Algoritmul G#

Eliminarea Gaussiană clasică, asemănătoare cu cea predată de obicei în cursurile de algebră liniară, poate fi ușor convertită într-un algoritm implementabil pe calculator.

Voi deschide acest subiect printr-o vizualizare simplă, iar apoi voi detalia o explicație analitică, un exemplu practic, o analiză a complexității și un cod ilustrativ.

Vizualizarea algoritmului#

Să explicăm întâi grafic algoritmul.

Fie \(A\in\mathbb{R}^{4\times4}\), o matrice pătratică de coeficienți pentru sistemul de ecuații liniare \(A\bm{x}=\bm{b}\), unde \(x,b\in\mathbb{R}^4\). Atunci sistemul ia forma:

\[ A\bm{x}=\bm{b}\Rightarrow\begin{bmatrix} a_{11} & \boxtimes & \boxtimes & \boxtimes \\ a_{21} & \boxtimes & \boxtimes & \boxtimes \\ a_{31} & \boxtimes & \boxtimes & \boxtimes \\ a_{41} & \boxtimes & \boxtimes & \boxtimes \end{bmatrix} \begin{bmatrix} x_1\\x_2\\x_3\\x_4 \end{bmatrix}=\begin{bmatrix} b_1\\b_2\\b_3\\b_4 \end{bmatrix}\Rightarrow\overline{A}=\begin{bmatrix} a_{11} & \boxtimes & \boxtimes & \boxtimes & b_1\\ a_{21} & \boxtimes & \boxtimes & \boxtimes & b_2 \\ a_{31} & \boxtimes & \boxtimes & \boxtimes & b_3 \\ a_{41} & \boxtimes & \boxtimes & \boxtimes & b_4 \end{bmatrix} \]

Am folosit simbolul "\(\boxtimes\)" pentru a marca acele valori ce nu prezintă interes. Totodată, am notat \(\overline{A}=\begin{bmatrix}A&\bm{b}\end{bmatrix}\) matricea extinsă, utilă descrierii sistemului printr-o prescurtare. În forma unui sistem de ecuații liniare, notația matriceală poate fi văzută drept:

\[ \begin{cases} a_{11}x_1&+\boxtimes x_2 + \boxtimes x_3 + \boxtimes x_4=b_1\\ a_{21}x_1&+\boxtimes x_2 + \boxtimes x_3 + \boxtimes x_4=b_2\\ a_{31}x_1&+\boxtimes x_2 + \boxtimes x_3 + \boxtimes x_4=b_3\\ a_{41}x_1&+\boxtimes x_2 + \boxtimes x_3 + \boxtimes x_4=b_4 \end{cases} \]

Transformarea primei ecuații în singura ce conține coeficienți nenuli pentru \(x_1\) se poate realiza în mai mulți pași, primul fiind de a scădea din a doua ecuație pe prima scalată cu \(\frac{a_{21}}{a_{11}}\). Astfel, se obține:

\[ \begin{cases} a_{11}x_1&+\boxtimes x_2 + \boxtimes x_3 + \boxtimes x_4=b_1\\ \,\,\,\,\,0&+\boxtimes x_2 + \boxtimes x_3 + \boxtimes x_4=b_2'\\ a_{31}x_1&+\boxtimes x_2 + \boxtimes x_3 + \boxtimes x_4=b_3\\ a_{41}x_1&+\boxtimes x_2 + \boxtimes x_3 + \boxtimes x_4=b_4 \end{cases}\Leftrightarrow\overline{A}=\begin{bmatrix} a_{11} & \boxtimes & \boxtimes & \boxtimes & b_1\\ 0 & \boxtimes & \boxtimes & \boxtimes & b_2' \\ a_{31} & \boxtimes & \boxtimes & \boxtimes & b_3 \\ a_{41} & \boxtimes & \boxtimes & \boxtimes & b_4 \end{bmatrix} \]

Aceste operații nu modifică soluția finală (vezi introducerea).

Continuând acest proces pentru cea de-a treia și cea de-a patra ecuație (considerând constantele \(\frac{a_{31}}{a_{11}}\), respectiv \(\frac{a_{41}}{a_{11}}\)), se va obține o singură ecuație ce conține un factor nenul pentru \(x_1\):

\[ \begin{cases} a_{11}x_1&+\boxtimes x_2 + \boxtimes x_3 + \boxtimes x_4=b_1\\ \,\,\,\,\,0&+\boxtimes x_2 + \boxtimes x_3 + \boxtimes x_4=b_2'\\ \,\,\,\,\,0&+\boxtimes x_2 + \boxtimes x_3 + \boxtimes x_4=b_3'\\ \,\,\,\,\,0&+\boxtimes x_2 + \boxtimes x_3 + \boxtimes x_4=b_4' \end{cases}\Leftrightarrow\overline{A}=\begin{bmatrix} a_{11} & \boxtimes & \boxtimes & \boxtimes & b_1\\ 0 & \boxtimes & \boxtimes & \boxtimes & b_2' \\ 0 & \boxtimes & \boxtimes & \boxtimes & b_3' \\ 0 & \boxtimes & \boxtimes & \boxtimes & b_4' \end{bmatrix} \]

Acest proces se poate repeta pentru \(x_2\) (pornind de la a doua linie) și \(x_3\) (începând cu a treia linie). Rezultatul va fi o matrice superior triunghiulară ce poate fi rezolvată foarte rapid (vezi rezolvarea sistemelor folosind LU):

\[ \begin{cases} a_{11}x_1+a_{12}x_2 + a_{13}x_3 + a_{14}x_4=b_1\\ a_{22} x_2 + a_{23} x_3 + a_{24} x_4=b_2'\\ a_{33} x_3 + a_{34} x_4=b_3''\\ a_{44} x_4=b_4''' \end{cases}\Leftrightarrow\overline{A}=\begin{bmatrix} a_{11} & a_{12} &a_{13} & a_{14} & b_1\\ 0 & a_{22} & a_{23} & a_{24} & b_2' \\ 0 & 0 & a_{33} & a_{34} & b_3'' \\ 0 & 0 & 0 & a_{44} & b_4''' \end{bmatrix} \]

Explicația algoritmică#

Să încercăm să formalizăm vizualizarea anterioară.

Fie \(A\bm{x}=\bm{b}\) un sistem de ecuații liniare, unde \(A\in\mathbb{R}^{n\times n}\) este o matrice pătratică și \(\bm{x},\bm{b}\in\mathbb{R}^n\) sunt vectori coloană. Notăm \(\overline{A}=\begin{bmatrix}A&\bm{b}\end{bmatrix}\) matricea extinsă ce conține elemente de forma \(\overline{a}_{ij}\) pe linia \(i\in\overline{1,n}\), coloana \(j\in\overline{1,n+1}\).

Pentru fiecare linie \(i\) cu excepția ultimei (\(i\in\overline{1,n-1}\)), vom transforma fiecare element aflat sub \(\overline{a}_{ii}\) (anume \(\overline{a}_{ji}\), \(\forall j\in\overline{i+1,n}\)) în zero prin scăderea celei de-a \(i\)-a linie înmulțită cu \(\frac{\overline{a}_{ji}}{\overline{a}_{ii}}\) din a \(j\)-a linie.

Matematic, algoritmul poate fi scris drept:

\[ \boxed{\bm{L_j}(\overline{A})\rightarrow \bm{L_j}(\overline{A})-\frac{\overline{a}_{ji}}{\overline{a}_{ii}}\cdot \bm{L_i}(\overline{A})}\,,\,\,\forall j\in\overline{i+1,n} \]

Notație

Pe parcursul acestui capitol, voi folosi destul de des notația \(\bm{L_k}(M)\) pentru a denota a \(k\)-a linie a matricei \(M\).

Spre exemplu, \(\bm{L_j}(\overline{A})=\begin{bmatrix}\overline{a}_{j1}&\dots&\overline{a}_{j,n+1}\end{bmatrix}\).

Același algoritm poate fi reutilizat pentru orice fel de matrice \(A\), nu trebuie să fie o matrice pătratică, dar rezultatul se poate dovedi a fi inutil. Vom reveni asupra acestei noțiuni ulterior.

Exemplificarea algoritmului#

Să considerăm următorul sistem de ecuații liniare, scris în formă matriceală: \( \begin{bmatrix} 1 & -2 & 1\\ 2 & 1 & -3\\ 4 & -7 & 1 \end{bmatrix}\begin{bmatrix} x_1\\x_2\\x_3 \end{bmatrix}=\begin{bmatrix} 0\\5\\1 \end{bmatrix}\). Știm deci \(\overline{A}=\begin{bmatrix} 1 & -2 & 1 & | & 0\\ 2 & 1 & -3 & | & 5\\ 4 & -7 & 1 & | & 1 \end{bmatrix}\).

Putem acum să urmăm pașii descriși algoritmic:

Pasul 1. Golirea primei coloane. Se execută:
\[ \begin{cases} \bm{L_2}(\overline{A})\rightarrow \bm{L_2}(\overline{A})-2 \bm{L_1}(\overline{A})\\ \bm{L_3}(\overline{A})\rightarrow \bm{L_3}(\overline{A})-4 \bm{L_1}(\overline{A}) \end{cases}\Rightarrow \overline{A}=\begin{bmatrix} 1 & -2 & 1 & | & 0\\ 0 & 5 & -5 & | & 5\\ 0 & 1 & -3 & | & 1 \end{bmatrix} \]
Pasul 2. Golirea celei de-a doua coloane. Se execută:
\[ \bm{L_3}(\overline{A})\rightarrow \bm{L_3}(\overline{A})-\dfrac{1}{5}\cdot \bm{L_2}(\overline{A}) \Rightarrow \overline{A}=\begin{bmatrix} 1 & -2 & 1 & | & 0\\ 0 & 5 & -5 & | & 5\\ 0 & 0 & -2 & | & 0 \end{bmatrix} \]

Concluzie. Se rezolvă sistemul superior triunghiular (de jos în sus) și se obține \( \begin{cases} x_3=0\\ x_2=1\\ x_1=2 \end{cases}\).

Cod ilustrativ#

Codul de mai jos implementează algoritmul G (funcția G), primind parametrii reprezentativi sistemului \(A\bm{x}=\bm{b}\):

A - matricea coeficienților sistemului;
b - vectorul coloană din partea dreaptă a egalității.

Funcția returnează perechea [A, b], echivalentul unui sistem triunghiular de ecuații liniare pe care se poate aplica apoi SST-ul explicat anterior.

function [A, b] = G(A, b)
    [m, n] = size(A);
    Ae = [A, b];
    for p = [1 : n-1]
        if (A(p ,p) == 0)
            continue;
        end
        for l = p+1 : n
            arg = Ae(l, p) / Ae(p, p);
            Ae(l, :) = Ae(l, :) - arg * Ae(p, :);
        end
    end
    A = Ae(:, 1:n);
    b = Ae(:, n+1);
end

Analiza complexității#

Fie \(GE_i(n,m)\) numărul de operații necesare pentru a calcula cel de-al \(i\)-lea pas. Pentru a transforma elementele \(\overline{a}_{i+1,i},\dots,\overline{a}_{n,i}\) în zero, toate liniile \(i+1,\dots, n\) trebuie reevaluate.

A \(j\)-a linie (\(j\in\overline{i+1,n}\)) va conține în acest moment exclusiv valori nule înaintea celei de-a \(i\)-a coloane, așadar elementele ce necesită o transformare se află pe pozițiile \(\overline{a}_{ji},\dots,\overline{a}_{jm}\). Dacă se consideră constant costul de înmulțire a unui număr cu un altul și de a scădea din rezultat o valoare, atunci \(GE_i(n,m)\) va lua valoarea:

\[\begin{split} GE_i(n,m)&=\sum_{j=i+1}^n(m-i+1)=(n-i)(m-i+1)\\ &= nm - ni - mi + n + i^2 - i\\ &= \left(nm + n\right) - (n+m+1)i + i^2 \end{split}\]

Cu toate acestea, dat fiind faptul că \(n\) și \(m\) pot fi două valori distincte (\(n\neq m\)), trebuie recalculat numărul de pași din algoritmul nostru. Vom ilustra cele trei posibilități în care ne putem afla:

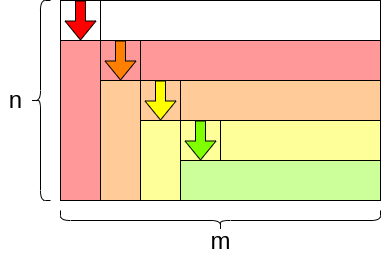
\(n\lt m\) (\(n-1\) pași)

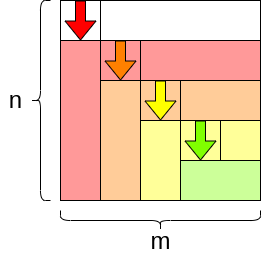
\(n=m\) (\(n-1\) steps)

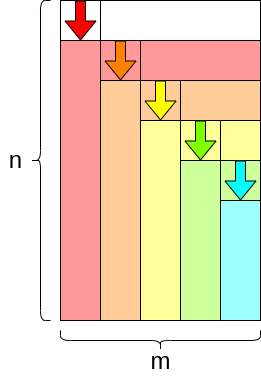
\(n\gt m\) (\(m\) steps)

După cum se poate observa în ilustrațiile de mai sus, se vor executa mereu \(\mu=\min\{n-1,m\}\). Așadar, costul total poate fi calculat drept suma tuturor acestor costuri mai mici. \(GE(n, m)\) va fi:

\[\begin{split} GE(n,m)&=\sum_{i=1}^{\mu}T_i(n,m)\\ &=\sum_{i=1}^{\mu}\left(nm + n\right) - (n+m+1)i + i^2\\ &= \sum_{i=1}^{\mu}\left(nm + n\right) - \sum_{i=1}^{\mu}(n+m+1)i + \sum_{i=1}^{\mu}i^2\\ &= \left(nm + n\right)\mu - (n+m+1)\cdot\frac{ \mu\cdot(\mu+1)}{2} +\frac{\mu\cdot(\mu+1)\cdot (2\mu+1)}{6} \end{split}\]

Astfel, complexitatea temporală a algoritmului poate fi interpretată drept \(O(mn\mu)= O(mn\cdot\min\{m,n\})\) - la aceasta, se va adăuga (dacă se dorește soluționarea unui sistem de ecuații liniare) complexitatea de a rezolva un SST (vezi rezolvarea SEL folosind LU). Complexitatea finală va fi deci dictată de eliminarea gaussiană, așadar \(O(mn\cdot\min\{m,n\})\).

Necesitatea unei îmbunătățiri#

Din nefericire, nu suntem pe deplin satisfăcuți de acest algoritm.

Să considerăm următorul sistem:

\[ A\bm{x}=\bm{b}\Rightarrow\begin{bmatrix} 0 & \boxtimes & \boxtimes \\ 1 & \boxtimes & \boxtimes \\ 0 & \boxtimes & \boxtimes \end{bmatrix} \begin{bmatrix} x_1\\x_2\\x_3 \end{bmatrix}=\begin{bmatrix} b_1\\b_2\\b_3 \end{bmatrix} \]

Deoarece elementul \(a_{11}\) este nul, în urma execuției algoritmului, pe prima coloană nu se va întâmpla nimic. Este deci nevoie de o modalitate de a îndrepta situația.

Vom explora o soluție în subcapitolul următor.

Licență#

The book "Metode Numerice", written by Valentin-Ioan Vintilă, is licensed under CC BY-NC-SA 4.0