Factorizarea Householder#

Precum la Gram-Schmidt, pornim de la un fundament matematic, de data aceasta poate un pic mai anevoios, iar apoi vom explica modalitatea prin care se realizează descompunerea QR folosind factorizarea Householder.

Reflectori Householder#

Începem cu o formulă care s-ar putea inițial să nu ne spună foarte multe, însă a cărei interpretare geometrică vom vedea că este extrem de intuitivă.

Fie un vector \(\bm{u}\in\mathbb{R}^n\), \(n\in\mathbb{N}^*\), cu norma sa euclidiană \(||\bm{u}||\). Atunci, se definește matricea \(H\in\mathbb{R}^{n\times n}\) astfel încât:

Prin definiție, matricea \(H\) poartă denumirea de reflector Householder (sau transformare Householder) asociat(ă) vectorului \(\bm{u}\).

Proprietăți matematice#

Câteva proprietăți utile când vine vorba despre acești reflectori sunt:

• Simetria. Reflectorii Householder sunt simetrici, adică \(\boxed{H=H^T}\)

  Demonstrație

  Realizăm calculul brut:

  \[\begin{split} H^T&=\left[I_n-2\cdot\frac{\bm{u}\bm{u}^T}{||\bm{u}||^2}\right]^T=I_n-2\cdot\frac{\left(\bm{u}\bm{u}^T\right)^T}{||\bm{u}||^2}=I_n-2\cdot\frac{\left(\bm{u}^T\right)^T\bm{u}^T}{||\bm{u}||^2}\\ &=I_n-2\cdot\frac{\bm{u}\bm{u}^T}{||\bm{u}||^2}=H \end{split}\]

• Ortogonalitatea și involuția. Un reflector Householder este caracterizat de egalitatea: \(\boxed{H^TH=HH^T=H^2=I_n}\)

  Demonstrație

  Deoarece \(H^T=H\), este evident că \(H^2=H^TH=HH^T\). Suplimentar:

  \[\begin{split} H^2&=\left[I_n-2\cdot\frac{\bm{u}\bm{u}^T}{||\bm{u}||^2}\right]^2=I_n-4\cdot\frac{\bm{u}\bm{u}^T}{||\bm{u}||^2}+\left[2\cdot\frac{\bm{u}\bm{u}^T}{||\bm{u}||^2}\right]^2\\ &=I_n-4\cdot\frac{\bm{u}\bm{u}^T}{||\bm{u}||^2}+4\cdot\frac{\bm{u}\left(\bm{u}^T\bm{u}\right)\bm{u}^T}{||\bm{u}||^4}\\ &=I_n-4\cdot\frac{\bm{u}\bm{u}^T}{||\bm{u}||^2}+4\cdot\frac{\bm{u}||\bm{u}||^2\bm{u}^T}{||\bm{u}||^4}\\ &=I_n-4\cdot\frac{\bm{u}\bm{u}^T}{||\bm{u}||^2}+4\cdot\frac{\bm{u}\bm{u}^T}{||\bm{u}||^2}=I_n \end{split}\]

Interpretarea geometrică#

Din punct de vedere geometric, produsul \(H\bm{x}\) (pentru vectorul coloană \(\bm{x}\in\mathbb{R}^n\), \(n\in\mathbb{N}^*\)) reflectă vectorul \(\bm{x}\) relativ față de planul perpendicular pe \(\bm{u}\).

Dacă \(\bm{v}\perp\bm{u}\), \(\bm{v}\in\mathbb{R}^n\), atunci \(H\bm{v}=\bm{v}\).

Ne apropiem ușor-ușor de interpretarea geometrică! Va trebui însă, pentru a simplifica matematica, să ne limităm la o explicație pentru subspațiul bidimensional.

Fie \(\bm{u}\in\mathbb{R}^2\) un vector coloană astfel încât \(||\bm{u}||=1\), respectiv \(\bm{v}\in\mathbb{R}^2\) astfel încât \(\bm{u}\perp\bm{v}\). Atunci, orice vector coloană \(x\in\mathbb{R}^2\) poate fi descompus drept suma:

unde \(\bm{x_v}\parallel\bm{v}\), respectiv \(\bm{x_u}\parallel\bm{u}\). În acest caz, se poate deduce că \(\bm{x_u}\) este proiecția lui \(\bm{x}\) pe \(\bm{u}\), iar \(\bm{x_v}\) este proiecția lui \(\bm{x}\) pe \(\bm{v}\).

Putem deci să scriem că:

Folosind toate aceste noțiuni și notații, se poate executa \(H\bm{x}\), unde \(H\in\mathbb{R}^{2\times 2}\) este un reflector Householder, iar \(\bm{x}\in\mathbb{R}^2\) este un vector oarecare:

În această situație, operația \(\bm{x}\rightarrow H\bm{x}\) este echivalentă cu operația \(\bm{x_v}+\bm{x_u}\rightarrow\bm{x_v}-\bm{x_u}\). Deoarece explicația analitică nu este pe deplin satisfăcătoare, propunem următoarea vizualizare:

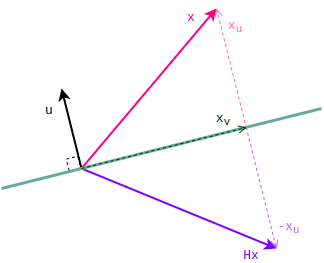
Interpretarea geometrică a reflectorului Householder. Cu turcoaz este desenat planul perpendicular vectorului \(\bm{u}\).

Calcularea reflectorului Householder#

Bun, dar cum obținem acest reflector?

Fie \(\bm{x},\bm{y}\in\mathbb{R}^n\), \(n\in\mathbb{N}^*\), alese astfel încât \(||\bm{x}||=||\bm{y}||\) și \(H\bm{x}=\bm{y}\), unde \(H\) este un reflector Householder. Atunci are loc egalitatea \(H=I_n-2\bm{u}\bm{u^T}\), unde \(\bm{u}\) se definește drept:

Avem tot ceea ce ne trebuie ca să începem să construim factorizarea Householder.

Fundamentul factorizării#

Reflectorii Householder sunt foarte utili pentru a transforma anumite elemente dintr-un vector \(\bm{a}\in\mathbb{R}^n\), \(n\in\mathbb{N}^*\), în zerouri.

Să considerăm o matrice oarecare \(A=\begin{bmatrix} \bm{a_1}&\bm{a_2}&\dots&\bm{a_n} \end{bmatrix}\in\mathbb{R}^{n\times n}\) și vectorul \(\bm{e_1}\) din baza subspațiului aritmetic \(\mathbb{R}^n\).

Dacă ne propunem să întocmim transformarea \(\bm{a_1}\rightarrow ||\bm{a_1}||\bm{e_1}\) folosind un reflector Householder, vom defini acest reflector \(H_1\) prin relația:

Astfel, aplicând înmulțirea \(H_1A\), se obține:

unde \(\bm{R_{1,2:n}}\) este un vector linie ce nu prezintă interes, respectiv \(B\in\mathbb{R}^{(n-1)\times(n-1)}\) reprezintă o matrice de dimensiune mai mică pe care se poate continua algoritmul recursiv.

Dacă apoi se consideră \(B=\begin{bmatrix} \bm{b}_2&\bm{b}_3&\dots&\bm{b}_n \end{bmatrix}\in\mathbb{R}^{(n-1)\times(n-1)}\) și \(\bm{e}_1\in\mathbb{R}^{n-1}\), transformarea \(\bm{b}_2\rightarrow ||\bm{b}_2||\bm{e}_1\) se poate realiza folosind reflectorul Householder \(\hat{H_2}\), unde:

și \(H_2=\begin{bmatrix} 1 & 0 \\ 0 & \hat{H_2} \end{bmatrix}\). Calculând \(\hat{H_2}B\), se obține:

Revenind la matricea inițială, rezultatul final ar fi:

Algoritmul poate continua deci recusiv.

Simplificarea vizuală#

Acest proces continuă până când se epuizează toate coloanele și funcționează inclusiv pentru matrice cu număr diferit de linii și de coloane. O exemplificare vizuală a algoritmului este dată de următoarea matrice oarecare \(A\in\mathbb{R}^{5\times4}\):

Factorizarea Householder#

Din exemplificarea de mai sus, se remarcă faptul că, dacă \(A=QR\) este factorizarea QR a matricei \(A\in\mathbb{R}^{n\times m}\), \(Q\in\mathbb{R}^{n\times n}\) și \(R\in\mathbb{R}^{n\times m}\), atunci valoarea lui \(R\) poate fi obținută prin:

unde \(\mu=\min\left\{m,n-1\right\}\) și \(H_i\) este definit folosind explicația anterioară. Totodată, folosind proprietățile reflectorilor Householder, observăm că:

Exemplificarea algoritmului#

Să considerăm matricea \(A=\begin{bmatrix}2 & 4 & 5\\1 & -1 & 1\\2 & 1 & -1\end{bmatrix}\). Fie \(A=QR\) descompunerea \(QR\) de tip Householder a matricei alese. Vom urma pașii descriși anterior:

• Pasul 1. Calcularea lui \(H_1\) și a matricei \(B\):

  Ne uităm la prima coloană a matricei \(A\) și observăm \(\bm{a_1}=\begin{bmatrix}2&1&2\end{bmatrix}^T\). Astfel, se poate calculaî \(\rho_1=||\bm{a_1}||=3\). Folosind aceste rezultate, obținem:

  \[ \bm{u_1}=\frac{\bm{a_1}-\rho_1\bm{e_1}}{||\bm{a_1}-\rho_1\bm{e_1}||}=\frac{1}{\sqrt{6}}\begin{bmatrix} -1\\1\\2 \end{bmatrix} \]

  Trecând la \(H_1=I_3-2\bm{u_1}\bm{u_1}^T\):

  \[ H_1=\begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix}-\frac{1}{3}\begin{bmatrix}-1\\1\\2\end{bmatrix}\begin{bmatrix}-1 & 1 & 2\end{bmatrix}=\frac{1}{3}\begin{bmatrix} 1 & -1 & -2\\ -1 & 1 & 2\\ -2 & 2 & 4 \end{bmatrix} \]

  Pentru a ajunge la matricea \(B\), vom calcula mai întâi \(H_1A\):

  \[ H_1A=\begin{bmatrix} 3 & 3 & 3\\ 0 & 0 & 3\\ 0 & 3 & 3 \end{bmatrix}\Rightarrow B=\begin{bmatrix} 0 & 3\\ 3 & 3 \end{bmatrix}\]

• Pasul 2. Calcularea lui \(H_2\) și a matricei \(R\):

  Observăm prima coloană a matricei \(B\), adică \(\bm{b_2}=\begin{bmatrix}0&3\end{bmatrix}^T\) cu norma \(||\bm{b_2}||=3\). Se poate deci calcula vectorul \(\bm{u_2}\):

  \[ \bm{u_2}=\frac{\bm{b_2}-\rho_2\bm{e_1}}{||\bm{b_2}-\rho_2\bm{e_1}||}=\frac{1}{\sqrt{2}}\begin{bmatrix} -1\\1 \end{bmatrix} \]

  Se calculează apoi \(\hat{H_2}\) și \(H_2\):

  \[ H_2=\begin{bmatrix} 1 & 0\\0 & 1 \end{bmatrix}-\begin{bmatrix} -1\\1 \end{bmatrix}\begin{bmatrix} -1&1 \end{bmatrix}=\begin{bmatrix} 0 & 1\\1&0 \end{bmatrix}\Rightarrow H_2=\begin{bmatrix} 1 & 0 & 0\\ 0 & 0 & 1\\0 & 1 & 0 \end{bmatrix} \]

  Pentru a ajunge la \(R\), se va calcula \(H_2H_1A\):

  \[ R=H_2H_1A=3\begin{bmatrix} 1 & 1 & 1\\0 & 1 & 1\\ 0 & 0 & 1 \end{bmatrix}\]

• Pasul 3. Calcularea matricei \(Q=H_1H_2=\dfrac{1}{3}\begin{bmatrix} 2 & 2 & 1\\1 & -2 & 2\\2 & -1 & -2 \end{bmatrix}\)

Așadar, factorizarea QR a matricei \(A\) este:

Cod ilustrativ#

Implementarea algoritmului Householder, inspirată din pseudocodul lui Jun Lu[26][27], va fi făcută în cadrul funcției householder, și va utiliza drept parametru matricea A, matricea de factorizat.

Funcția returnează perechea [Q, R], unde am notat:

• Q - matricea ortogonală din factorizarea QR;

• R - matricea superior triunghiulară a factorizării QR.

Evident, se respectă egalitatea \(A=QR\).

function [Q, R] = householder(A)
    [m, n] = size(A);
    R = A;
    Q = eye(m);
    for i = [1 : n-1]
        a = R(i:m, i);
        r = norm(a);
        u_i = a - r * eye(m-i+1, 1);
        u_i = u_i / norm(u_i);

        R(i, i) = r; R(i+1:m, i) = 0;
        R(i:m,i+1:n) = R(i:m, i+1:n) - 2 * u_i * (u_i' * R(i:m,i+1:n));

        Q(1:m, i:m) = Q(1:m, i:m) - Q(1:m, i:m) * 2 * u_i * u_i';
    end
end

Analiza complexității#

Calcularea unui reflector Householder la fiecare pas \(i\in\overline{1,\mu}\) necesită un produs vectorial între doi vectori coloană de lungime \((n-i+1)\), respectiv multiple produse de tip vector-matrice, deci ne așteptăm la o complexitate de \(O(mn)\) la fiecare pas \(i\).

Așadar, în total complexitatea temporală va fi \(O(mn\mu)\).

Licență#

The book "Metode Numerice", written by Valentin-Ioan Vintilă, is licensed under CC BY-NC-SA 4.0