Factorizarea Givens#

Dintre toate factorizările QR, factorizarea Givens este de departe cea mai ușor de înțeles și de vizualizat, fiind extrem de geometrică. Cu toate acestea, propunem cititorilor să treacă mai întâi prin materialul scris pentru Householder.

Matrice de rotație 2D#

Algebra liniară este strâns legată de geometria analitică. Din acest motiv, există matrice de rotație cu ajutorul cărora, prin înmulțirea cu un vector coloană, acesta poate fi rotit.

Fie \(\bm{x}\in\mathbb{R}^2\) un vector oarecare din subspațiul bidimensional ce formează un unghi \(\theta\in\mathbb{R}\) față de abscisă (\(Ox\)). Se dorește rotirea acestui vector cu \(\varphi\in\mathbb{R}\) radiani, fie în sens trigonometric, fie în sensul acelor de ceasornic, adică se dorește transformarea \(\bm{x}\rightarrow\bm{y}\), unde \(\bm{y}\in\mathbb{R}^2\) este un vector ce formează un unghi \(\theta\pm\varphi\) cu abscisa.

Pentru a îndeplini această cerință, vom considera matricele \(J_\varphi,G_\varphi\in\mathbb{R}^{2\times2}\) definite astfel:

Operația \(J_\varphi\bm{x}\) va avea ca efect rotirea vectorului \(\bm{x}\) cu \(\varphi\) radiani în sens trigonometric, iar operația \(G_\varphi\bm{x}\) va rezulta în rotirea vectorului \(\bm{x}\) cu \(\varphi\) radiani în sensul acelor de ceasornic.

Conceptul de rotire a unui vector este foarte intuitiv din punct de vedere grafic, așadar propunem următoarea ilustrație:

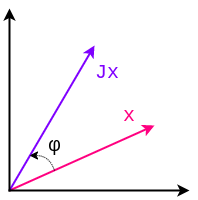
Rotirea lui \(\bm{x}\) în sens trigonometric cu \(\varphi\) radiani, folosind matricea \(J\), adică \(J\bm{x}\).

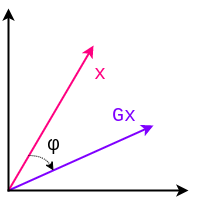
Rotirea lui \(\bm{x}\) în sensul acelor de ceasornic cu \(\varphi\) radiani, folosind matricea \(G\), adică \(G\bm{x}\).

Eliminarea unei coordonate#

Folosind aceste matrice, putem elimina elemente specifice ale unui vector coloană dat.

Fie \(\bm{x}=\begin{bmatrix} x_1\\x_2 \end{bmatrix}\) și \(y=\begin{bmatrix} ||\bm{x}||\\0 \end{bmatrix}\) doi vectori aleși astfel încât \(G\bm{x}=\bm{y}\), unde \(\bm{x},\bm{y}\in\mathbb{R}^2\), iar \(G\) este o matrice de rotație în sens invers trigonometric. Se vor cristaliza următoarele relații fundamentale:

Se poate verifica faptul că sistemul anterior este corect:

Așadar, folosind matricea \(G\), putem elimina una din componentele vectorului \(\bm{x}\) (în cazul \(\bm{x}\rightarrow\bm{y}\), se elimină a doua coordonată).

Matrice de rotație Givens#

Cele două matrice de rotație prezentate anterior, \(J_\varphi\) și \(G_\varphi\), reprezintă particularizări pentru \(\mathbb{R}^2\) ale matricelor de rotație Givens. Pentru a generaliza, definim matricele de rotație \(J_{ij},G_{ij}\in\mathbb{R}^{n\times n}\), unde \(n\in\mathbb{N}^*\), \(\forall i\in\overline{1,n-1},\,j\in\overline{i+1,n}\), ce își propun rotirea unui vector din \(\mathbb{R}^n\) cu \(\varphi\in\mathbb{R}\) radiani în planul definit de coordonatele \(i\) și \(j\).

Acestea iau formele:

1. Matricea \(\,\,\boxed{J_{ij}=\begin{bmatrix} 1 & \dots & 0 & \dots & 0 & \dots & 0 \\ \vdots & \ddots & \vdots & \ddots & \vdots & \ddots & \vdots \\ 0 & \dots & \cos\varphi & \dots & -\sin\varphi & \dots & 0 \\ \vdots & \ddots & \vdots & \ddots & \vdots & \ddots & \vdots \\ 0 & \dots & \sin\varphi & \dots & \cos\varphi & \dots & 0 \\ \vdots & \ddots & \vdots & \ddots & \vdots & \ddots & \vdots \\ 0 & \dots & 0 & \dots & 0 & \dots & 1 \end{bmatrix}}\,\,\) va conține elemente de forma: \(j_{ab}=\begin{cases} \cos\varphi,&a=b=i\text{ sau }a=b=j \\ -\sin\varphi,&a=i,\,b=j\\ \sin\varphi,&a=j,\,b=i\\ 1,&a=b,\,a\neq i,\,a\neq j\\ 0,&\text{în rest} \end{cases}\)

2. Matricea \(\,\, \boxed{ G_{ij}=\begin{bmatrix} 1 & \dots & 0 & \dots & 0 & \dots & 0 \\ \vdots & \ddots & \vdots & \ddots & \vdots & \ddots & \vdots \\ 0 & \dots & \cos\varphi & \dots & \sin\varphi & \dots & 0 \\ \vdots & \ddots & \vdots & \ddots & \vdots & \ddots & \vdots \\ 0 & \dots & -\sin\varphi & \dots & \cos\varphi & \dots & 0 \\ \vdots & \ddots & \vdots & \ddots & \vdots & \ddots & \vdots \\ 0 & \dots & 0 & \dots & 0 & \dots & 1 \end{bmatrix} } \,\,\) va conține elemente de forma: \( g_{ab}=\begin{cases} \cos\varphi,&a=b=i\text{ sau }a=b=j \\ \sin\varphi,&a=i,\,b=j\\ -\sin\varphi,&a=j,\,b=i\\ 1,&a=b,\,a\neq i,\,a\neq j\\ 0,&\text{în rest} \end{cases}\)

Formarea matricei de rotație \(G\)#

În baza sistemului anterior și renunțând la rigoarea matematică, pentru a forma matricea \(G_{ij}\), \(\forall i\in\overline{1,n-1},\,j\in\overline{i+1,n}\):

1. Se pornește de la matricea \(I_{n}\);

2. Se înlocuiesc elementele de pe diagonala principală aflate pe pozițiile \((i,i)\), respectiv \((j,j)\) cu valoarea lui \(\cos\varphi\);

3. Elementele ce au fost modificate formează în mod unic un pătrat cu colțurile rămase \((i,j)\), respectiv \((j,i)\), iar acestea devin:

   • Deasupra diagonalei principale: \(\sin\varphi\);

   • Sub diagonala pincipală: \(-\sin\varphi\).

Influența asupra unui vector oarecare#

O matrice Givens de rotație \(G_{ij}\) (sau \(J_{ij}\)) are ca efect asupra unui vector oarecare \(\bm{x}\in\mathbb{R}^n\), \(n\in\mathbb{N}^*\), rotirea sa cu \(\varphi\in\mathbb{R}\) radiani în planul determinat de vectorii de indici \(i\) și \(j\).

Înmulțirea cu \(G_{ij}\) (sau \(J_{ij}\)) a unui vector oarecare \(\bm{x}\in\mathbb{R}^n\), \(\bm{x}=\begin{bmatrix} x_1\\x_2\\\vdots\\x_n \end{bmatrix}\), unde \(n\in\mathbb{N}^*\), are ca efect schimbarea a numai două elemente componente ale vectorului, \(x_i\) și \(x_j\).

Eliminarea unei coordonate#

Folosind proprietatea demonstrată anterior, transformarea unui vector oarecare \(\bm{x}\in\mathbb{R}^n\), \(n\in\mathbb{N}^*\), astfel încât acesta să își piardă coordonata \(j\) (adică aceasta să devină nulă) prin înmulțirea cu matricea de transformare Givens \(G_{ij}\), \(\forall i\in\overline{1,n-1},\,j\in\overline{i+1,n}\), va avea loc astfel:

Așadar, aplicarea transformării compuse \((G_{1n}\dots G_{13}G_{12})\bm{x}\) asupra unui vector oarecare \(\bm{x}\in\mathbb{R}^n\), \(n\in\mathbb{N}^*\), are ca efect transformarea \(\bm{x}\rightarrow||\bm{x}||\bm{e}_1\). Acest lucru se poate arăta prin aplicarea transformărilor pe rând:

Continuând pe un raționament inductiv, se obține:

Se obține deci că: \( \boxed{\left(G_{1n}\dots G_{13}G_{12}\right) \bm{x}=||\bm{x}||\bm{e}_1}\).

Generalizarea pe matrice#

Putem face ușor trecerea de la vectori coloană la matrice.

Fie \(A=\begin{bmatrix} \bm{a}_1&\bm{a}_2&\dots&\bm{a}_n \end{bmatrix}\in\mathbb{R}^{n\times n}\), \(n\in\mathbb{N}^*\). Folosind proprietatea dovedită mai sus, se poate defini transformarea compusă:

ce are ca efect eliminarea tuturor elementelor aflate pe prima coloană, cu excepția primului. Așadar, aplicând transformarea pe matricea \(A\), se obține:

unde \(\bm{R_{1,2:n}}\in\mathbb{R}^{(n-1)}\) este un vector linie ce nu prezintă interes, respectiv \(B\in\mathbb{R}^{(n-1)\times(n-1)}\) reprezintă o matrice de dimensiune mai mică pe care se poate continua algoritmul recursiv.

Asemănător algoritmului Householder, dacă, în continuare, se consideră matricea mai mică \(B=\begin{bmatrix} \bm{b}_2&\bm{b}_3&\dots&\bm{b}_n \end{bmatrix}\in\mathbb{R}^{(n-1)\times(n-1)}\) și \(\bm{e}_1\in\mathbb{R}^{n-1}\), atunci transformarea \(\bm{b}_2\rightarrow||\bm{b}_2||\bm{e}_1\) se poate realiza folosindu-ne de produsul:

Astfel, aplicând înmulțirea următoare:

se poate reveni la matricea inițială \(A\):

Cu toate că acest algoritm este complet valid, în ceea ce privește procesul didactic, se va folosi o versiune ușor modificată, făcând transformările direct pe matricea \(A\) și ignorând crearea unor matrice intermediare (a se vedea exemplul de mai jos).

Simplificarea vizuală#

Acest proces continuă până când se epuizează toate coloanele și funcționează inclusiv pentru matrice cu număr diferit de linii și de coloane. O exemplificare vizuală a algoritmului este dată de următoarea matrice oarecare \(A\in\mathbb{R}^{5\times4}\):

Grupând în funcție de \(G_k=G_{k,5}\dots G_{k,k+2} G_{k,k+1}\), \(\forall k\in\overline{1,4}\), se obține:

Factorizarea Givens#

Din exemplificarea de mai sus, se remarcă faptul că, dacă \(A=QR\) este factoizarea \(QR\) a matricei \(A\in\mathbb{R}^{n\times n}\), \(n\in\mathbb{N}^*\), atunci valoarea lui \(R\) poate fi obținută prin:

Pentru a calcula matricea \(Q\), se va folosi formula:

Exemplificarea algoritmului#

Să considerăm matricea \(A = \begin{bmatrix} 0 & -1 & 1\\ 4 & 2 & 0\\ 3 & 4 & 0 \end{bmatrix}\). Fie \(A=QR\) descompunerea sa QR de tip Givens. Vom urma pașii descriși anterior:

• Pasul 1. Calcularea lui \(G_1=G_{13}G_{12}\):

  \(G_1\) va fi compus la rândul lui din \(G_{12}\) și \(G_{13}\) ce vor trebui aflate separat Începem cu \(G_{12}\):

  \[ \bm{x}=\begin{bmatrix} x_1=0\\x_2=4 \end{bmatrix}\Rightarrow G_{12}=\begin{bmatrix} \cos\varphi & \sin\varphi & 0\\ -\sin\varphi & \cos\varphi & 0\\ 0 & 0 & 1 \end{bmatrix},\,\begin{cases} \cos\varphi=\frac{x_1}{||\bm{x}||}=0\\ \sin\varphi=\frac{x_2}{||\bm{x}||}=1 \end{cases} \]

  Pentru a putea continua, avem nevoie de noua matrice \(A\), adică \(G_{12}A\):

  \[ G_{12}A = \begin{bmatrix} 0 & 1 & 0\\ -1 & 0 & 0\\ 0 & 0 & 1 \end{bmatrix}\cdot\begin{bmatrix} 0 & -1 & 1\\ 4 & 2 & 0\\ 3 & 4 & 0 \end{bmatrix}=\begin{bmatrix} 4 & 2 & 0\\ 0 & -1 & 1\\ 3 & 4 & 0 \end{bmatrix} \]

  Putem acum să îl calculăm pe \(G_{13}\):

  \[ \bm{x}=\begin{bmatrix} x_1=4\\x_2=3 \end{bmatrix}\Rightarrow G_{13}=\begin{bmatrix} \cos\varphi & \sin\varphi & 0\\ 0 & 1 & 0 \\ -\sin\varphi & \cos\varphi & 0 \end{bmatrix},\,\begin{cases} \cos\varphi=\frac{x_1}{||\bm{x}||}=0.8\\ \sin\varphi=\frac{x_2}{||\bm{x}||}=0.6 \end{cases} \]

• Pasul 2. Calcularea lui \(G_2=G_{23}\):

  Matricea pe care se vor executa calculele viitoare este dată de formula:

  \[ (G_{13}\cdot G_{12})A = \begin{bmatrix} 0.6 & 0 & 0.8\\ 0 & 1 & 0\\ -0.8 & 0 & 0.6 \end{bmatrix}\cdot\begin{bmatrix} 4 & 2 & 0\\ 0 & -1 & 1\\ 3 & 4 & 0 \end{bmatrix}=\begin{bmatrix} 5 & 4 & 0\\ 0 & 1 & -1\\ 0 & 2 & 0 \end{bmatrix} \]

  Folosind rezultatele anterioare, se obține sistemul:

  \[ \bm{x}=\begin{bmatrix} x_1=1\\x_2=2 \end{bmatrix}\Rightarrow G_{23}=\begin{bmatrix} 1 & 0 & 0\\ 0 & \cos\varphi & \sin\varphi\\ 0 & -\sin\varphi & \cos\varphi \end{bmatrix},\,\begin{cases} \cos\varphi=\frac{x_1}{||\bm{x}||}\approx0.447\\ \sin\varphi=\frac{x_2}{||x||}\approx0.894 \end{cases} \]

• Pasul 3. Calcularea lui \(R\) și a lui \(Q\):

  Matricea \(R\) este dată de formula \(R=(G_2\cdot G_1)A=(G_{23}\cdot G_{13}\cdot G_{12})A\), deci:

  \[ R\approx \begin{bmatrix} 1 & 0 & 0\\ 0 & 0.447 & 0.894\\ 0 & -0.894 & 0.447 \end{bmatrix}\cdot\begin{bmatrix} 5 & 4 & 0\\ 0 & 1 & -1\\ 0 & 2 & 0 \end{bmatrix}\approx\begin{bmatrix} 5 & 4 & 0\\ 0 & 2.236 & -0.447\\ 0 & 0 & 0.897 \end{bmatrix} \]

  Nu în ultimul rând, \(Q=G_1^T\cdot G_2^T=G_{12}^T\cdot G_{13}^T\cdot G_{23}^T\), deci:

  \[\begin{split} Q&\approx\begin{bmatrix} 0 & 1 & 0\\ -1 & 0 & 0\\ 0 & 0 & 1 \end{bmatrix}\cdot\begin{bmatrix} 0.6 & 0 & 0.8\\ 0 & 1 & 0\\ -0.8 & 0 & 0.6 \end{bmatrix}\cdot\begin{bmatrix} 1 & 0 & 0\\ 0 & 0.447 & 0.894\\ 0 & -0.894 & 0.447 \end{bmatrix}\\&\approx\begin{bmatrix} 0 & -0.447 & 0.894\\ 0.8 & -0.537 & -0.268\\ 0.6 & 0.716 & 0.358 \end{bmatrix} \end{split}\]

Așadar, factorizarea QR a matricei \(A\) este:

Cod ilustrativ#

Implementarea algoritmului Givens sub forma funcției givens (pe matrice oarecare) presupune notația A pentru matricea pe care o vrem factorizată.

Funcția returnează perechea [Q, R], unde am notat:

• Q - matricea ortogonală din factorizarea QR;

• R - matricea superior triunghiulară a factorizării QR.

Evident, se respectă egalitatea \(A=QR\).

function [Q, R] = givens(A)
    [n, m] = size(A);
    Q = eye(m);

    for j = [1 : min(n-1, m)]
        for k = [j + 1 : n]
            rho = sqrt(A(j,j)^2 + A(k,j)^2);
            c = A(j,j) / rho;
            s = -A(k,j) / rho;

            aux = [c -s; s c] * [A(j, j:m); A(k, j:m)];
            A(j, j:m) = aux(1, :);
            A(k, j:m) = aux(2, :);

            aux = [c -s; s c] * [Q(j, 1:n); Q(k, 1:n)];
            Q(j, 1:n) = aux(1, :);
            Q(k, 1:n) = aux(2, :);
        end
    end

    Q = Q';
    R = A;
end

Analiza complexității#

Deoarece fiecare transformare de forma \(G_{ij}\) presupune produse scalare între vectori de lungime \(n\), iar în total sunt aproximativ \(\sum_{i=1}^n(n-i)=O(n^2)\) transformări, complexitatea finală este aproximativ \(O(n^3)\).

Concluzie#

Acest tip de factorizare poate fi util în situația în care încercăm să găsim scrierea QR a unei matrice sparse (matrice rară). Cu toate acestea, datorită stabilității numerice deosebite, chiar și în această situație preferăm utilizarea factorizării Householder.

Licență#

The book "Metode Numerice", written by Valentin-Ioan Vintilă, is licensed under CC BY-NC-SA 4.0